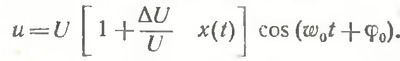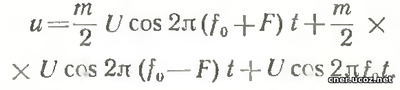Сайт "Cner"

Сокращенное название однополосной модуляции (SSB), принятое в радиолюбительском коде, происходит от английского Single Side Band, что в переводе означает — одна боковая полоса.

Прежде чем приступить к рассмотрению однополосной модуляции, вспомним, что представляет собой модуляция вообще. При этом мы не будем пока касаться методов ее осуществления.

Модуляцией называется процесс изменения одного или нескольких параметров данного сигнала под воздействием другого сигнала.

Модулируемый сигнал обычно представляет собой простейшие колебания, которые описываются выражением: u=Ucos(ωt+φ₀), где U — амплитуда; ω₀=2пf₀— угловая частота; φ₀—начальная фаза; t— время.

Параметрами такого сигнала являются амплитуда U, частота ω₀ (или f₀) и фаза φ₀.

Низкочастотный сигнал X(t), воздействующий на один из этих параметров, называется модулирующим сигналом. В зависимости от того, на какой из параметров воздействует такой сигнал, различают три вида модуляции: амплитудную, частотную и фазовую.

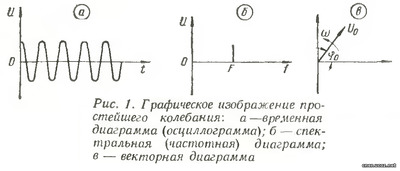
Для анализа модулированных колебаний будем пользоваться тремя различными представлениями о сигнале: временным, спектральным (частотным) и векторным. В соответствии с этими представлениями косинусоидальное (или синусоидальное) колебание, записанное выше,— графически можно представить так, как показано на рис. 1.

На рис. 1,a по оси абсцисс отложено время t, а по оси ординат — мгновенное значение амплитуды U. На рис. 1, б по оси абсцисс отложена частота f=ω/2п, по оси ординат - амплитуда. На этом графике синусоидальное колебание изображается в виде отрезка прямой линии, параллельной оси ординат. Длина отрезка соответствует амплитуде колебания U, а его положение на оси абсцисс— частоте f₀. На рис. 1. в синусоидальное колебание представлено в виде вектора, вращающегося против часовой стрелки с угловой скоростью   ω₀=2пf₀=2п/Т₀, где Т₀— период колебания. Длина вектора соответствует амплитуде U, я угол φ₀ — начальной фазе, при которой начат отсчет времени.

Следует отметить, что все три представления о модулирующем сигнале совершенно равносильны Мы будем пользоваться каждым из них или несколькими представлениями параллельно, когда это окажется наиболее подходящим.

Рассмотрим амплитудную модуляцию. В этом случае амплитуда U высокочастотных колебаний изменяется во времени в соответствии с передаваемым низкочастотным сигналом U_m=U + ΔUx(t), где ΔU—постоянная величина, характеризующая интенсивность воздействия модулирующего сигнала на амплитуду. Подставив в первое выражение значение амплитуды U_m получим:

Отношение ΔU/U=m, характеризующее глубину модуляции, называется коэффициентом модуляции.

Если модулирующий сигнал изменяется по закону X(t) =cosΩt, где Ω=2пf, F—частота модулирующего сигнала, то, считая начальную фазу ф₀ равной нулю, можно записать:

Раскрыв скобки и проведя преобразование, получим:

Последнее равенство представляет собой сумму трех косинусоидальных колебаний, а именно, первоначальное колебание (без учета фазы ф₀) с частотой f₀, или так называемая несущая, колебания с частотой f₀+F - верхняя боковая частота и колебания с частотой f₀—F - нижняя боковая частота. Амплитуды боковых колебаний равны между собой и пропорциональны амплитуде несущей и коэффициенту модуляции.

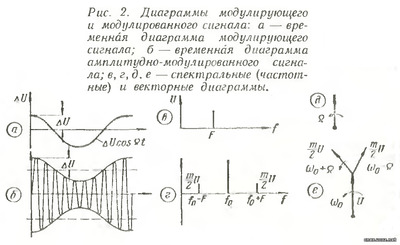
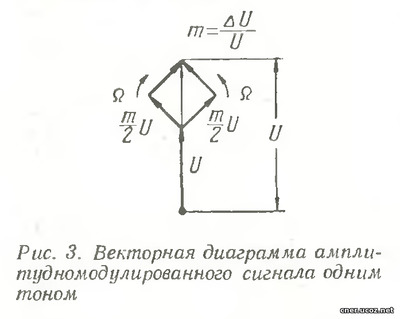
На рис. 2, а показаны временные, спектральные и векторные диаграммы модулирующего и модулированного сигналов, как видно из рис. 2,б огибающая модулированного колебания полностью повторяет первоначальный сигнал. Векторную диаграмму рис. 2, е удобнее представить несколько иначе. Если наблюдатель будет вращаться в плоскости чертежа со скоростью вектора несущей, то этот вектор будет казаться ему неподвижным, а векторы, соответствующие верхним и нижним боковым частотам, будут вращаться в противоположные стороны с угловой скоростью Ω. Амплитуда результирующего вектора изменяется во времени по закону низкой частоты, а фаза совпадает с фазой несущего колебания (рис. 3).

При частотной и фазовой модуляции длина вектора U остается постоянной. Изменяется во времени его положение на плоскости. Вектор как бы качается относительно первоначального положения. Угол отклонения Δф называется девиацией фазы. Отклонение частоты Δf от своего номинального значения f₀ называется девиацией частоты.

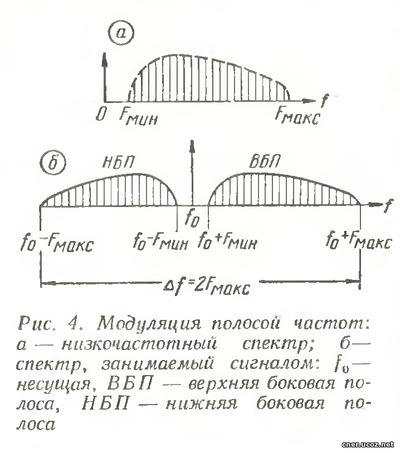
Разница между частотной и фазовой модуляцией заключается в том, что при фазовой модуляции мгновенное изменение фазового угла происходит по закону изменения низкочастотного сигнала, а при частотной модуляции по такому закону изменяется мгновенная частота. Определить, является ли данный сигнал частотномодулированным или фазомодулированным, можно только в том случае, если известен закон изменения низкочастотного сигнала. Между обоими видами модуляции существует вполне определенная математическая зависимость. В обоих случаях вектор, соответствующий модулированному сигналу, вращается вокруг своего начала не равномерно, а с некоторой переменной угловой скоростью.

Мы рассмотрели модуляцию одним низкочастотным сигналом (одним тоном). Представляет интерес случай, когда модулирующий сигнал является не простым гармоническим, а более сложным, например, содержащим три или больше частот. В этом случае говорят не о боковых частотах, а о боковых полосах модуляции. При модуляции речевым сигналом, представляющим сложное колебание, обладающее широким частотным спектром, образуются нижняя и верхняя боковые полосы. Если низшей частотой модуляции является F_мин, а высшей F_макс, то весь спектр, занимаемый амплитудномодулируемым сигналом (AM), будет равен 2F_макс. (рис. 4).

Исследование сигналов AM колебаний показывает, что полезная информация заключается в любой из двух боковых полос модуляции, а несущая никакой полезной информации не имеет. В передатчике на несущую тратится значительная часть мощности, что делает AM модуляцию малоэффективной.

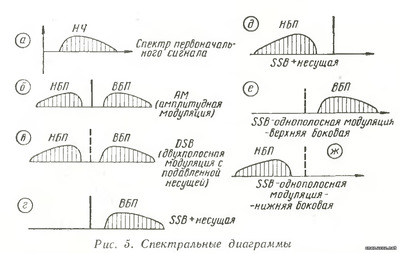
Очевидно, для передачи нужной информации можно ограничиться передачей только одной из боковых полос. Несущую можно восстанавливать в приемнике с помощью местного маломощного гетеродина. При этом будет экономиться не только энергия, затрачиваемая на питание передатчика, но и сузится полоса частот, занимаемая сигналом.

Некоторый интерес представляют собой также передача двух боковых полос без несущей (DSB) и одной боковой с несущей. Поэтому, рассматривая однополосную модуляцию (ОМ), затронем также и эти виды модуляции.

На рис. 5 представлена частотная диаграмма первоначального спектра передаваемого сигнала, AM, DSB, SSB с несущей и SSB без несущей. Однополосный сигнал может быть образован с сохранением взаимного расположения частотных составляющих спектра, как показано на рис. 5, е и 5, г или с переворачиванием (инверсией) спектра (рис. 5, д и 5, ж). В первом случае однополосный спектр сигнала называют верхней боковой полосой или нормальным спектром, во втором случае — нижней боковой или инвертированным спектром.

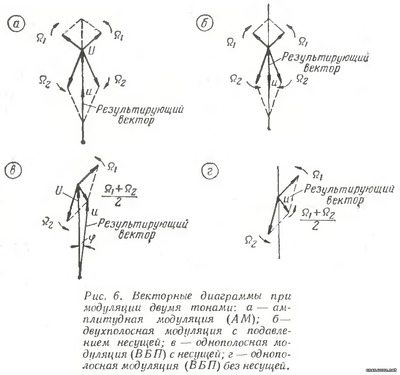
На рис. 6 приведены векторные диаграммы AM, DSB, SSB с несущей и SSB без несущей при модуляции спектром, состоящим из двух частотных составляющих Ω₁ и Ω₂. Вектор несущей заторможен. При AM (рис. 6, а) имеем вектор несущей и две пары векторов, соответствующих двум верхним и двум нижним боковым частотам. Результирующий вектор совпадает по фазе с вектором несущей.

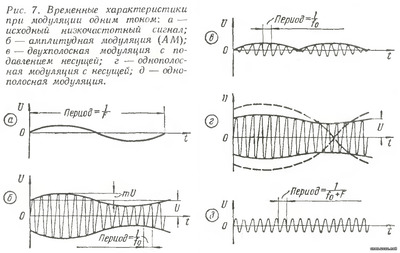
При DSB (рис. 6, б) отсутствует вектор несущей. Поэтому результирующий вектор либо совпадает с вектором подавленной несущей, либо направлен в противоположную сторону, т. е. сдвинут по фазе на 180°. На рисунке показан случай, когда результирующий вектор как раз направлен в противоположную сторону.

На рис. 6, в показана диаграмма однополосного сигнала с несущей. Обе составляющие верхней боковой полосы представлены двумя векторами, вращающимися в одну и ту же сторону с угловыми скоростями Ω₁ и Ω₂. Суммарный вектор с угловой скоростью (Ω₁+Ω₂)/2, складываясь с вектором несущей, образует результирующий вектор v. Как видно из графика, этот вектор «качается» относительно первоначального положения и изменяет свою длину. Таким образом, в случае однополосной модуляции с несущей имеет место комбинированная амплитудно-частотная модуляция.

На рис. 6, г дана векторная диаграмма однополосного двухтонального сигнала. Результирующий вектор в этом случае представляет собой вектор, вращающийся со скоростью (Ω₁+Ω₂)/2 против часовой стрелки. Так как один из векторов все время «догоняет» другой, то амплитуда результирующего вектора изменяется. Отсюда можно сделать также вывод, что однополосная модуляция представляет собой комбинированную амплитудно-частотную модуляцию. Исследования показывают, что при однополосной модуляции амплитуда изменяется по закону изменения мгновенных амплитуд модулирующего сигнала, а частота — по закону изменения его мгновенной частоты.

Очень важную практическую роль играют временные характеристики рассмотренных выше сигналов, поскольку с ними приходится сталкиваться при налаживании SSB возбудителей с помощью осциллографа. Поэтому рассмотрим подробно сначала временные характеристики при модуляции одним тоном (рис. 7), а затем двумя тонами (рис. 8).

Исходный синусоидальный сигнал низкой частоты показан на рис. 7, а. Диаграмму AM сигнала (рис. 7, б) легко построить, пользуясь векторной диаграммой рис. 3. Фаза огибающей AM сигнала совпадает с фазой исходного сигнала в течение всего периода модуляции.

На рис. 7, в приведена диаграмма двухполосного сигнала, построенная в соответствии с рис. 2, но при векторе несущей, равном нулю. Вращающиеся в противоположные стороны векторы дважды за один оборот (за период Т=1/F) складываются арифметически и дважды компенсируют друг друга. Поэтому модуль  результирующего вектора изменяется синусоидально, а фаза в течение одной половины периода модулирующего сигнала совпадает с фазой подавленной несущей, в течение же другой половины — опрокидывается. Так как амплитуда — величина положительная, то огибающая двухполосного сигнала без несущей представляет собой синусоиду, отрицательная половина которой повернута на 180° вокруг оси времени. Высокочастотное заполнение осциллограммы представляет собой колебание с частотой f₀, фаза которого опрокидывается при переходе модулирующего напряжения через ноль.

Пользуясь той же векторной диаграммой AM колебания, но отбросив один из векторов, соответствующей боковой частоте, можно легко построить осциллограмму однополосного сигнала с несущей. Огибающая в этом случае так же не соответствует первоначальному сигналу, причем искажения огибающей будут тем больше, чем глубже модуляция. На рисунке пунктиром показана огибающая при стопроцентной модуляции. Частота заполнения изменяется в течение периода низкой частоты.

На рис. 7,д изображена диаграмма однополосного сигнала без несущей. Диаграмма представляет собой обычный синусоидальный сигнал, (огибающая прямая линия), с постоянной амплитудой, с частотой ω₀+F или ω₀—F. Чем глубже модуляция, тем больше амплитуда сигнала.

Рассмотрим временные диаграммы двухчастотного сигнала. Для упрощения построения возьмем два сигнала с одинаковой амплитудой и кратными частотами F₁ и  F₂= 3F₁. На рис. 8,а сплошной линией представлен модулирующий сигнал, в состав которого входят колебания с указанными частотами. На рис. 8,б показана диаграмма амплитудно-модулированного сигнала. Его огибающая соответствует модулирующему сигналу.

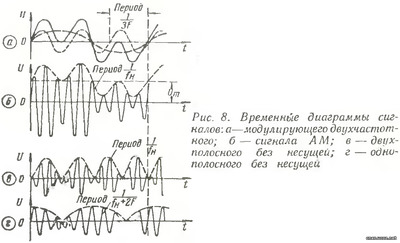
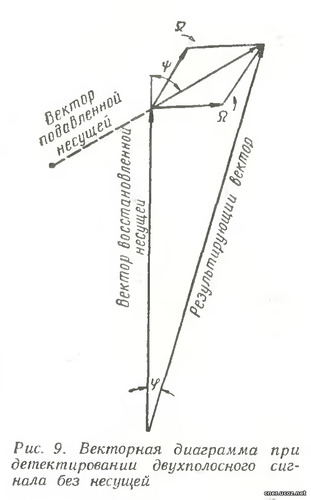
Диаграмму двухполосного сигнала без несущей (рис. 8,в) можно построить рассуждая так же, как в случае одночастотного сигнала. В течение тех промежутков времени, когда модулирующее напряжение положительно, фаза огибающей соответствует фазе модулирующего напряжения, а фаза высокочастотного заполнения совпадает с фазой подавленной несущей. При отрицательном модулирующем напряжении фазы огибающей и высокочастотного заполнения опрокидываются. Частота заполнения в обеих случаях равна частоте несущей f₀. Временную диаграмму двухтонального однополосного сигнала можно построить и проанализировать, обратившись к соответствующей диаграмме рис. 6. В нашем случае вектора, вращающиеся со скоростью и Ω₁=2пF₁ и Ω₂=2п(3F₁)= 3Ω₁ имеют одинаковую амплитуду, поэтому результирующий вектор будет вращаться равномерно со скоростью Ω₃=(Ω₁+3Ω₁)/2=2Ω₁. В начальный момент, когда оба вектора совпадают, длина результирующего вектора будет максимальной. Следовательно, амплитуда огибающей будет иметь удвоенную величину относительно амплитуд каждой из высокочастотных составляющих. В течение одного оборота вектора, угловая скорость которого Ω₁, вектор с угловой скоростью Ω₂=3Ω₁, дважды «догонит» первый вектор и два раза окажется направленным в противоположную сторону. В соответствии с этим длина результирующего вектора за период Т₁=1/F три раза окажется равной удвоенной амплитуде высокочастотных колебаний и два раза равной нулю.

Временная диаграмма для данного случая показана на рис. 8, в, Частота высокочастотного заполнения равна f₀+F₃=f₀+2F₁. Необходимо отметить, что в спектре колебаний, показанных на рис. 8,в колебания с частотой «заполнения», т. е. с частотой несущей, отсутствуют. Также нет в составе спектра сложного колебания, временная диаграмма которого изображена на рис 8,г, составляющей частоты f₀+2F.

При амплитудном детектировании рассмотренных выше сигналов на выходе детектора будет напряжение, соответствующее огибающей высокочастотных колебаний. В случае AM огибающая повторяет исходный сигнал, поэтому на выходе детектора появится модулирующий первоначальный сигнал низкой частоты. Детектирование однополосного сигнала с несущей также приведет к появлению на выходе детектора напряжения, соответствующего огибающей. Но, так как сама огибающая не точно воспроизводит модулирующий сигнал, то и продуктом детектирования будет сигнал искаженный, причем, чем глубже модуляция, тем больше искажения.

Ясно, что обычное детектирование DSB или SSB даст одни искажения. Например, при модуляции одним тоном F детектирование DSB приведет к появлению сигнала с удвоенной частотой 2F₁, и его гармоник, а детектирование SSB даст только постоянную составляющую.

Детектирование DSB и SSB, как было отмечено выше, производится с помощью местного гетеродина, восстанавливающего несущую. Интересно отметить, что восстановление частоты несущей в случае DSB должно выполняться с точностью до фазы (если конечно приемник пропускает обе боковые). В противном случае появляются нежелательные явления. Процесс детектирования иллюстрируется векторной диаграммой (рис. 9), на которой восстановленная несущая отличается по фазе от подавленной несущей на некоторый угол Ψ. При этом изменение длины суммарного вектора становится меньше, в результате чего эффект детектирования уменьшается. При сдвиге фазы на угол f=90° амплитудное детектирование никакого напряжения низкой частоты на выходе не даст.

Детектирование SSB с восстановленной в приемнике несущей в принципе не отличается от детектирования однополосного сигнала с неподавленной несущей.

Однако на форму выходного сигнала (огибающей) в этом случае, как было выяснено выше, влияет соотношение между амплитудой сигнала гетеродина и амплитудой детектируемого сигнала. Очевидно, искажения будут незначительны, когда амплитуда напряжения гетеродина во много раз будет больше амплитуды детектируемого сигнала. В этом можно убедиться, рассматривая временную диаграмму однополосного сигнала с неподавленной несущей (рис. 7,г).