| Главная » Статьи » Другие статьи » Статьи из литературы |
Частота
| Статья опубликована в ж. «Приборы и системы управления», 1978, №3, с. 19-20 в порядке дискуссии.
Известное положение В.И. Ленина - «перед человеком сеть явлений природы... Категории суть... узловые пункты в сети, помогающие познавать ее и овладевать ею» (Ленин В.И. ПСС 5-е изд. Т.29, с. 85) — в полной мере можно отнести и к таким научным понятиям, как физические величины. Познавательное значение каждой величины тем больше, чем больше число ее связей с другими величинами (другими узлами сети), чем в большем числе разнокачественных явлений она обнаруживается. Естественно, что в различных связях проявляются различные стороны величины, она как бы приобретает тонкую структуру, расщепляется на несколько близких по содержанию величин с самостоятельными определениями. Так обстоит дело, например с массой (тяжелой и инертной) или добротностью, определяемой по отношению энергий, ширине резонансного пика и крутизне фазо-частотной характеристики. Подобную же «тонкую структуру» имеет частота — величина, которая приобрела особое значение в связи с широким развитием частотных методов измерения, передачи и обработки информации. Фактически существуют четыре определения частоты, которым предлагается дать названия: хронометрическое, статистическое, фазовое, спектральное определения. Соответствующие «разновидности» частоты — хронометрическая, статистическая, фазовая и спектральная — совпадают только для бесконечного гармонического сигнала, физически не реализуемого. Как показывает опыт, смешение этих четырех понятий запутывает даже опытных разработчиков частотно-цифровых измерительных систем и приводит к ошибкам при их проектировании; поэтому необходимы точные формулировки всех определений применительно к физически реализуемым сигналам. Хронометрическую частоту (ХЧ) предлагается определять как величину fx=1/T, обратную периоду Т сигнала х(t), периодического на ограниченном интервале времени (t1, t2). Математически это означает, что X(t)=X(t+T) при всех значениях t, удовлетворяющих условиям t€(t1, t2), (t+T)€(t1+t2). Для того чтобы можно было убедиться в справедливости этого равенства для всех значений t в пределах периода, должно быть t2-t1>=2T. Конечно, в действительности равенство оказывается приближенным из-за неизбежных флуктуаций сигнала. Хронометрическая частота может быть приписана и непериодическим сигналам, если они поддаются преобразованию в периодические. Так, сигнал свободных затухающих колебаний изохронной системы преобразуется в периодический сигнал путем глубокого ограничения или делением на экспоненциальную функцию времени. Свойства ХЧ: каждый сигнал на заданном интервале имеет либо одну ХЧ (при условии, что за период принимается только наименьшая из положительных величин Т, при которых выполняется приведенное выше равенство), либо ни одной, причем в силу того что интервал должен содержать не менее двух периодов, ХЧ надо рассматривать как постоянную, а не как усредненную величину, ХЧ вещественна и всегда положительна. Адекватным измерением ХЧ является корреляционный метод — нахождение временного сдвига сигнала, при котором он совпадает с самим собой. Единица ХЧ — обратная секунда. Фазовую частоту (ФЧ) предлагается определять как скорость смены циклически чередующихся состояний источника сигнала. Если для применения понятия ХЧ нужна периодичность сигнала, то для применения понятия ФЧ достаточно более слабого условия цикличности, т.е. многократного прохождения сигналом (точнее источником сигнала) одной и той же последовательности состояний безотносительно к необходимому для этого времени. Данное время для разных циклов может быть различным (и тогда не следует называть его периодом). Средняя за цикл ФЧ есть величина, обратная времени, которое требуется сигналу на возвращение к определенному, легко узнаваемому состоянию, например к переходу через нуль в определенном направлении. Для выявления мгновенной ФЧ внутри цикла вводится понятие фазы как координаты процесса на цикле состояний источника; таким образом, ФЧ характеризует не столько сигнал, сколько его источник (по крайней мере ее нельзя определить по одному только виду сигнала, не зная устройства источника). Если источником сигнала x(t)=XmsinV(t) является гармоническая колебательная система, то ФЧ находится обычным образом как W=dV/dt; (для такой ФЧ принято особое название: круговая или угловая частота) или fф=(1/2¶)*( dV/dt); коэффициент 1/2¶ не нужен, если выражать фазу не в радианах, а в естественных единицах — циклах. Для изучения устройств с управляемыми негармоническими источниками сигнала предлагалось [1] вводить фиктивный гармонический источник, управляемый по тому же закону, что и исследуемый; это сводится к тому, что ФЧ приписывается непосредственно негармоническому источнику [2], однако это можно сделать не для всех источников, так как в сигнале не всегда содержится информация, необходимая для равномерного разбиения цикла состояний источника при любом управляющем воздействии. Свойства ФЧ: если сигналу определённого источника можно приписать ФЧ, то только одну; ФЧ характеризует сигнал в каждый момент и является непрерывной функцией времени, что делает её незаменимой при изучении процессов частотной модуляции; ФЧ вещественна, но может быть как положительной, так и отрицательной, если возможно обратное направление процесса в источнике. До недавнего времени такими источниками сигналов с потенциально знакопеременной ФЧ были только вращающиеся генераторы, а также смесители, выделяющие разностную частоту двух сигналов. Сейчас известно уже достаточно много разновидностей интегрирующих преобразователей напряжения в частоту, входное напряжение которых может менять полярность, что приводит к изменению направления интегрирования, а следовательно, и знака ФЧ. Адекватное измерение ФЧ связано с нахождением мгновенной фазы сигнала; применяемые при этом методы (близкие к хорошо разработанным методам интерполяции внутри кванта пространственных шкал [3]), как правило, требуют сигнала , состоящего из нескольких отдельных компонент, например синусоидальной и косинусоидальной. В некоторых случаях могут быть использованы структурные свойства сигнала; так, ФЧ гармонического неуправляемого источника может быть вычислена из соотношения: 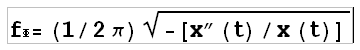 Единицы ФЧ: радиан в секунду и цикл в секунду (CPS – cycle per second).
Статистическая частота (СтЧ) определяется как число событий одного класса в единицу времени: fст=N/To. При этом полная идентичность событий необязательна, например это могут быть импульсы разных амплитуды и длительности. Один и тот же процесс может содержать несколько различных классов событий, для которых представляет интерес определение СтЧ: нули, экстремумы, выбросы и т.д. Чаще всего событием считается пересечение сигналом нулевого уровня в определённом направлении. Для СтЧ в связи с необходимостью её использования в теории функций Уолша предложены особые названия: частость [4] и постота (sequency) [5]. Частость выражается в пересечениях нуля в секунду (zps — zero crassing per second) [4]. Свойства СтЧ: каждому сигналу, за исключением физически нереализуемой последовательности бесконечно коротких импульсов одинаковой амплитуды, можно приписать не одну, а несколько СтЧ, различным образом определяя множества считаемых событий; СтЧ сама по себе, при отсутствии дополнительных сведений о сигнале характеризует его только на достаточно большом отрезке времени; однако, используя скользящее усреднение, можно рассматривать СтЧ как непрерывную функцию времени. Теоретически возможен, например, пуассоновский источник событий с интенсивностью µ(t), изменяющейся во времени как угодно быстро; но экспериментально, по одной реализации процесса обнаруживаются только медленные изменения СтЧ, являющейся оценкой интенсивности: fст(t)=µ(t). Статистическая частота вещественна и положительна. Прибором, адекватно определяющем СтЧ, служит цифровой частотомер (как известно, показания последнего могут быть различными в зависимости от уровня дискриминации). При этом СтЧ может определяться как счетом числа событий N при заданном интервале To , так и измерением интервала времени ТN , за который происходит заранее заданное число событий No , с последующим вычислением обратной величины. Если выбрать No=1, т.е. Измерять интервал между двумя смежными событиями, то СтЧ внешне сближается с ХЧ и со средней ФЧ за цикл; однако это сближение кажущееся, и говорить об изменении ХЧ или средней ФЧ цифровым частотомером можно только в том случае, если имеются дополнительные сведения, подтверждающие периодичность или цикличность исследуемого процесса, так как сам цифровой частотомер не проверяет ни того, ни другого. Единица СтЧ — событие в секунду времени (EPUT – event per unit time). Спектральная частота (СпЧ) качественно определяется как свойство сигнала воздействовать на определённым образом настроенные резонаторы и другие избирательные системы, а также наоборот — как резонаторы и другие избирательные системы, а также наоборот — как свойство избирательных систем отзываться на какие-то конкретные сигналы. Таким образом, если ФЧ характеризует сигнал со стороны источника, то СпЧ характеризует его со стороны приёмника, причём она может описывать приёмник и в невозбуждённом состоянии, значит, своего рода пассивный, мёртвый, скрытый сигнал (как, известно, работа многих частотных датчиков основана на выявлении и «оживлении» частоты, на которую настроена некоторая избирательная система). Из всех «разновидностей» частоты СпЧ в наименьшей степени связана с временем и в наибольшей демонстрирует особую сущность частоты как самостоятельной величины, поэтому именно она заслуживает выражения в специальных единицах — герцах. Количественно СпЧ определяется из преобразования Фурье всего сигнала или некоторой его части, которая подвергается наблюдению и анализу [6]; в последнем случае говорят о текущем спектре. Свойства СпЧ: всякий реальный сигнал, флуктуирующий и ограниченный во времени, занимает некоторую полосу спектральных частот: СпЧ характеризует сигнал в целом или по крайней мере достаточно большой его отрезок То , причём если сигнал в целом занимает узкую полосу СпЧ, то по мере уменьшения То эта полоса расширяется примерно как 1/ То ; СпЧ может быть как положительной, так и отрицательной. Адекватными средствами измерения СпЧ являются такие приборы, как волномер, резонансный герцметр, спектроанализатор. Все четыре рассмотренных понятия характеризует в общем одно и тоже объективное свойство сигналов — их «плотность» во времени, но с различных сторон, поэтому вряд ли разумно утверждать, что одно из четырёх определений истинно, а остальные ложны. Вот несколько примеров расхождения этих определений. Сигнал в виде отрезка синусоиды, формируемый гармоническим источником, имеет вполне свои и равные друг другу ХЧ и ФЧ, но занимает полосу СпЧ, а его СтЧ (частость) определяется путём счёта пересечений нуля с дискретностью того же порядка, что и ширина полосы СпЧ. У сигнала в виде периодически повторяющихся пар импульсов , СтЧ вдвое выше, чем ХЧ, а спектральных частот множество. Если говорить о ФЧ, то имеет некоторый смысл высказывание о том, что частота импульсов изменилась в середине интервала между импульсами (при этом имеется ввиду частота непрерывного процесса в источнике импульсов), а в отношении ХЧ, СтЧ и СпЧ это высказывание нелепо. Общее положение «самым быстрым способом получения информации о входной величине частотно-импульсного датчика является измерение периода его выходного сигнала» справедливо для датчиков, характеризуемых ХЧ, но неверно не только для датчиков со статистически распределёнными импульсами, но и для датчиков, выходные импульсы которых «привязаны» к определённым точкам временной шкалы. Естественно, что в анализе процессов, связанных с преобразованием спектров, должна участвовать только СпЧ. Практика разработки измерительных информационных систем с частотно-импульсным представлением информации требует, чтобы все четыре определения частоты могли использоваться на равных правах (конечно, каждый раз с указанием на то, какое из них имеется в виду). Целесообразно закрепить их законодательно, например в ГОСТ «Измерение времени и частоты. Термины и определения», одновременно оговорив виды сигналов, на которые они распространяются, и основные способы измерения. Многое из того, что было сказано выше, может быть отнесено также к терминологии в области вращательного движения, где существуют аналогичные трудности. Л И Т Е Р А Т У Р А 1. Ширман Я. Д. Частотные спектры при временной (фазовой) и частотной импульсной модуляции. - «Радиотехника», 1946, т.1, № 7-8. 2. Кнорринг В.Г. О механизме работы измерительных преобразователей с частотным выходом. - «Измерительная техника», 1966, №8. 3. Фотоэлектрические преобразователи информации. Под ред. Л.Н. Преснухина. -М.: Машиностроение, 1974. 4. Хармут Х.Ф. Передача информации ортогональными функциями. - М.: Связь, 1975. 5. Блюмин С.Л., Шмырин А.М. О простоте функций Уолша и их обобщений.- «Проблемы передачи информации», 1974, т. Х, № 3. 6. Харкевич А.А. Спектры и анализ. -М.: Физматгиз, 1962. 7. Джаков Э.С. О понятии «оборот».- «Измерительная техника», 1976, № 5. Автор: Вадим Глебович Кнорринг, доктор технических наук, профессор кафедры Измерительных информационных технологий Санкт-Петербургского государственного политехнического университета. Источник публикации: ж. «Приборы и системы управления», 1978, № 3, с. 19-20. | |
| Просмотров: 1230 | |