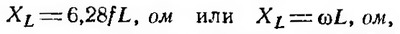Приветствую Вас, Гость! Регистрация RSS

Сайт "Cner"

Суббота, 20.04.2024
Главная » Статьи » Другие статьи » Радиолюбительские статьи
Индуктивность в цепи переменного тока
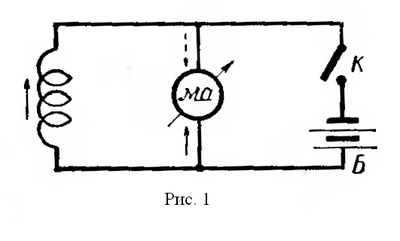
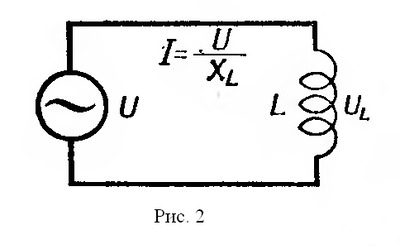
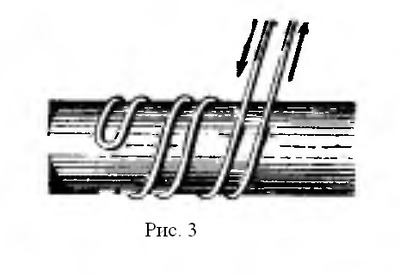
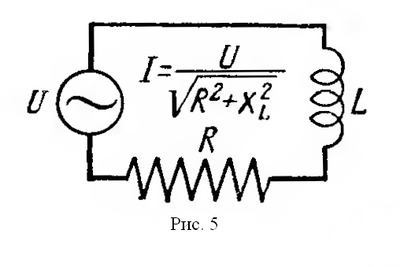
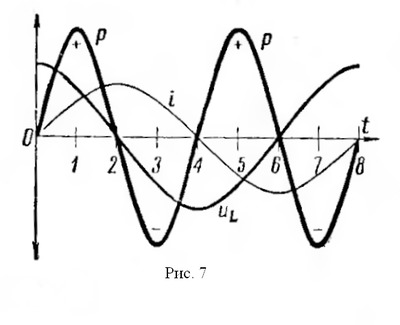
Самоиндукция.

Если в замкнутом контуре течет непостоянный ток, то магнитное поле, создаваемое этим током, также непостоянно. В проводе (катушке) под влиянием изменения ее собственного магнитного потока индуктируется ЭДС, называемая ЭДС самоиндукции. Согласно закону Ленца, ЭДС самоиндукции всегда противоположна вызвавшей ее причине. Если ток в цепи возрастает, то ЭДС самоиндукции стремится замедлить нарастание тока. Если ток в цепи уменьшается, ЭДС самоиндукции препятствует спаданию тока.

Характерным примером явления самоиндукции служат так называемые экстратоки замыкания и размыкания. При питании цепей постоянным током ЭДС самоиндукции возникает и оказывает влияние на изменение тока только в моменты замыкания и размыкания цепи (рис.1).
В проводниках различной формы величина ЭДС самоиндукции различна. Прямолинейный проводник имеет слабое магнитное поле и поэтому ЭДС самоиндукции невелика. Она заметно сказывается только в очень длинных проводниках или при очень быстрых изменениях тока. Значительная ЭДС возникает в проводниках, образующих катушку.

Индуктивность L характеризуется величиной ЭДС самоиндукции, возникающей в катушке при изменении величины тока на один ампер в секунду. Единицей измерения индуктивности является генри (Гн).

При включении в цепь переменного тока катушки индуктивности (рис.2) образуется переменное магнитное поле и в витках катушки наводится ЭДС самоиндукции. Для создания и поддержания переменного тока в цепи катушки необходимо преодолеть действие ЭДС самоиндукции.
Сопротивление, которое вносит в цепь переменного тока катушка индуктивности, называется индуктивным сопротивлением. Индуктивное сопротивление возникает вместе с появлением ЭДС самоиндукции, а величина последней зависит от величины индуктивности L и скорости изменения магнитного потока в катушке, то есть скорости изменения величины тока в ней. Таким образом индуктивное сопротивление зависит от частоты переменного тока. Чем больше частота переменного тока, тем больше индуктивное сопротивление катушки.

Реактивное сопротивление катушки зависит от индуктивности катушки (числа витков, формы и конструкции катушки) и пропорционально частоте переменного тока. Поэтому там, где необходимо получить возможно большее сопротивление переменному току, для увеличения магнитного потока через катушку применяются сердечники из различных магнитных материалов.

В тех случаях, когда необходимо иметь катушку с очень малой индуктивностью, применяют бифилярную намотку (рис.3). При такой намотке в каждых двух соседних витках ток имеет противоположное направление и суммарный магнитный поток равен нулю.
Всякий проводник или катушка обладают также и активным сопротивлением, но иногда для упрощения считают, что катушка обладает только индуктивным сопротивлением. Такую индуктивность считают идеальной.

Предположим, что идеальная индуктивность L подключена к источнику переменного тока в тот момент, когда его напряжение равно амплитудному значению. Ток в катушке не сразу достигнет амплитудного значения (рис. 4), так как возникающая в ней ЭДС самоиндукции uL всегда противоположна по фазе напряжению источника тока u и противодействует нарастанию тока. В результате процесс нарастания тока до амплитудного значения замедляется на время, равное одной четверти периода. Ток в цепи, содержащей чисто индуктивное сопротивление, отстает от напряжения на четверть периода или 90º.

Величина индуктивного сопротивления выражается следующей формулой:
где f — частота тока, гц; L — индуктивность катушки, гн;  ω — угловая частота.
Если включить в цепь переменного тока последовательно индуктивное и активное сопротивление (рис. 5), полное сопротивление такой цепи будет равно геометрической сумме сопротивлений; его можно определить по формуле: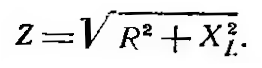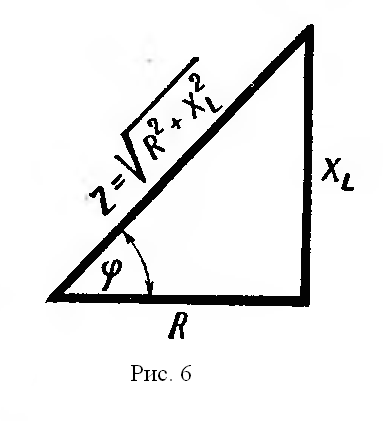
Это же вычисление можно произвести и графическим методом, построив прямоугольный треугольник, катеты которого по длине соответствуют величинам активного и индуктивного сопротивлений. Гипотенуза этого треугольника будет соответствовать величине полного сопротивления (рис. 6).
В цепи, содержащей индуктивное и активное сопротивления, сдвиг фаз между током и напряжением меньше 90° и зависит от отношения величины активного сопротивления к величине полного сопротивления R/Z. Из треугольника сопротивлений видно, что R/Z=cos  φ. Если XL значительно больше R, сдвиг по фазе будет приблизительно равен 90°, а если наоборот — R значительно превосходит XL, то сдвиг по фазе будет близким к нулю.

Если подсчитать мгновенные значения мощности как произведения мгновенных значений тока и напряжения по формуле p = ui и построить в некотором масштабе график мощности, то мы получим синусоиду, частота которой в два раза больше частоты проходящего по катушке тока. Энергия, поступающая в катушку индуктивности в течение первой и третьей четверти периода, идет на образование магнитного поля. Однако в течение второй и четвертой четверти периода магнитное поле отдает эту запасенную энергию обратно в цепь источника тока (рис. 7).
Как известно, мощность, потребляемая чисто активным сопротивлением, равняется произведению действующих значений тока и напряжения. Мощность. потребляемая чисто индуктивным сопротивлением, за период равна нулю. Для цепи, содержащей R и XL  потребляемая мощность зависит от соотношения этих величин. Чем меньше сдвиг фаз между током и напряжением, тем большую мощность потребляет цепь.

Величина мощности определяется по формуле: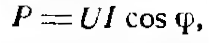
где U и I действующие значения тока и напряжения.
 
Мощность переменного тока, поглощаемую нагрузкой, называют активной и измеряют в ваттах (Вт) или киловаттах (кВт).

Произведение величины тока в цепи, содержащей индуктивность, на величину напряжения на ее зажимах измеряют в вольтамперах (ВА) и называют кажущейся мощностью.

Мощность, отдаваемая источником в течение одной части периода и возвращаемая в течение другой части периода, называется реактивной мощностью. Величина этой мощности определяется по формуле: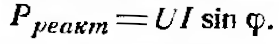
Категория: Радиолюбительские статьи | Добавил: cner (04.08.2017)
Просмотров: 1740 | Рейтинг: 0.0/0