| Главная » Статьи » Другие статьи » Статьи из литературы |
Распространение электромагнитной энергии
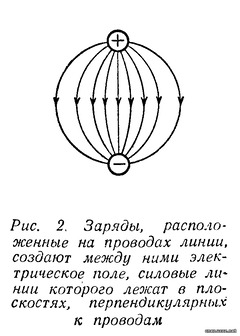
| Способы передачи электромагнитной энергии на расстояние по проводам и без них на первый взгляд кажутся принципиально различными и обычно их принято противопоставлять друг другу. Однако в действительности между ними есть много общего, так как в их основе лежат одни и те же законы распространения электромагнитной энергии. Эти общие законы были открыты выдающимся русским ученым профессором Московского университета Н. А. Умовым. Вот почему, несмотря на существенные различия между этими двумя случаями распространения электромагнитной энергии, правильнее их не противопоставлять, а сопоставлять между собой, т. е. рассматривать их с общей точки зрения тех единых принципов, которые были открыты Н. А. Умовым. Электрическое и магнитное поле постоянного тока Как известно, электромагнитная энергия сосредоточена в электрическом и магнитном полях, т. е. распределена с некоторой плотностью в пространстве, где действуют электрические и магнитные силы. Плотностью энергии называется отношение количества энергии, заключенной в каком-либо объеме, к величине этого объема, или, иначе говоря, количество энергии, отнесенное к единице объема. Поэтому, чтобы проследить за картиной распространения энергии, нужно рассмотреть электрические и магнитные поля, возникающие в том или ином конкретном случае. Для этого следует воспользоваться количественными характеристиками названных полей. Электрическое и магнитное поля в каждой точке определяются вектором напряженности поля. Вектор, как известно, есть «направленная величина», т. е. величина, имеющая не только определенное абсолютное значение, но и определенное направление в пространстве. Векторную величину можно изобразить при помощи отрезка (стрелки), направление которого совпадает с направлением заданного вектора, а длина в определенном выбранном масштабе выражает абсолютное значение этого вектора. В частности, вектор напряженности поля (электрического или магнитного) по направлению совпадает с направлением поля, а по абсолютной величине равен (в определенном масштабе) значению напряженности поля в данной точке. Изображая векторы напряженности при помощи отрезков (стрелок), можно графически изобразить распределение поля в пространстве. Этот способ изображения поля с помощью векторов легко связать с обычным методом изображения поля с помощью силовых линий. Так как направление силовых линий в каждой точке совпадает с направлением поля, стрелка, изображающая вектор напряженности поля в каждой точке, направлена по касательной к силовой линии, проходящей через эту точку. С другой стороны, так как густота силовых линий в данной точке поля пропорциональна напряженности поля в этой точке, то стрелки длиннее там, где силовые линии гуще, и короче, где силовые линии реже. Этим способом изображения полей с помощью векторов напряженности поля мы дальше будем широко пользоваться. Изучение картины распространения энергии мы начнем с простейшего случая передачи электромагнитной энергии по двум проводам с помощью постоянного тока. Прежде всего выясним, какие электрические и магнитные поля возникают в этом случае. Пусть двухпроводная линия присоединена одним концом к источнику постоянной ЭДС Е, а на другой ее конец включается какая-то нагрузка R (рис. 1). . 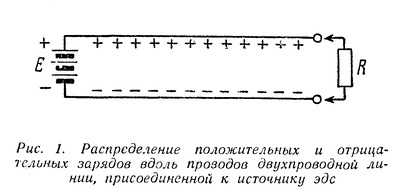 Пока нагрузка не включена, линия зарядится от источника ЭДС до напряжения U, равного Е, и между ее проводами, как и между всякими разноименно заряженными телами, возникнет электрическое поле. Это поле будет сосредоточено главным образом между самими проводами линии, быстро убывая по мере удаления от них. Вид этого поля в сечении, перпендикулярном к линии, примерно изображен на рис. 2. Поскольку разность потенциалов между проводами во всех сечениях линии (пока линия разомкнута) одна и та же, во всех сечениях между ее проводами будет существовать одинаковое электрическое поле. Здесь, как и всегда в электростатических случаях, силовые линии поля возле самого проводника будут перпендикулярны его поверхности (Что они должны быть перпендикулярны к поверхности, будет показано ниже.), и значит в продольном сечении линии электрическое поле будет иметь вид, изображенный на рис. 3. 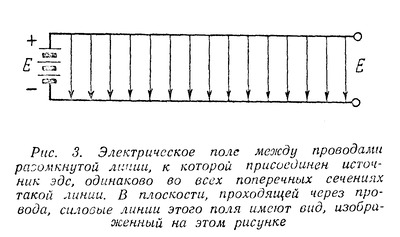 Перейдем теперь от электростатического поля к случаю, когда к концу линии подключена нагрузка R и значит в линии течет ток. Для того, чтобы облегчить этот переход, предположим сначала, что линия не обладает сопротивлением. Тогда, несмотря на наличие тока в линии, падения напряжения вдоль нее не будет и разность потенциалов между проводами по прежнему во всех сечениях останется одна и та же. А если распределение потенциалов вдоль линии не изменится, то не изменится и электрическое поле вокруг нее. Следовательно, если бы линия не обладала сопротивлением, то электрическое поле вокруг нее имело бы вид, изображенный для статического случая на рис. 2 и 3. Однако вследствие того, что линия в действительности обладает сопротивлением, при возникновении тока в ней картина электрического поля существенно изменится. Вдоль линии будет происходить падение напряжения, следовательно, разность потенциалов между ее проводами будет постепенно уменьшаться по мере удаления от источника ЭДС к концу линии, в который включена нагрузка. Поэтому электрическое поле между проводами будет в том же направлении постепенно ослабевать. Кроме того, изменится конфигурация поля. Чтобы выяснить этот вопрос, нам придется сделать небольшое отступление и рассмотреть картину электрического поля в самом проводе, по которому течет ток. В случае, когда заряды в проводнике неподвижны, электрическое поле внутри него отсутствует. В самом деле, если внутри проводника есть электрическое поле, оно должно вызывать в нем движение зарядов, причем последние будут двигаться до тех пор, пока электрическое поле внутри проводника не исчезнет. Иначе говоря, в электростатическом случае заряды распределяются по проводнику так, что создают электрическое поле только вне проводника; внутри него электрическое поле отсутствует. Кроме того, заряды на поверхности проводника распределяются так, что электрическое поле перпендикулярно к его поверхности. Если бы этого не было, то на поверхности проводника существовала бы составляющая электрического поля вдоль поверхности. Под действием этой составляющей поля заряды двигались бы вдоль поверхности. Итак, в случае неподвижных зарядов электрическое поле внутри проводника отсутствует, а снаружи проводника оно перпендикулярно к его поверхности. В случае же, когда заряды в проводнике все время движутся, картина существенно меняется. Так как всякий проводник обладает сопротивлением, то для непрерывного движения в нем зарядов (т. е. протекания электрического тока) на последние должны все время действовать силы, иначе говоря, внутри проводника должно существовать электрическое поле, направленное вдоль проводника и в ту же сторону, в которую течет ток. При этом вдоль проводника в направлении прохождения тока будет происходить падение потенциала. Таким образом, наличие электрического поля внутри проводника и падение потенциала вдоль проводника тесно связаны между собой. Это две стороны одного и того же явления. Но если существует электрическое поле внутри проводника, то оно существует и на его поверхности, убывая по мере удаления от него. В двухпроводной линии токи текут в противоположные стороны и, следовательно, электрические поля внутри проводников также направлены в противоположные стороны. Вне проводников эти поля постепенно убывают, так что получается непрерывный переход от внутреннего поля одного проводника к внутреннему полю другого. 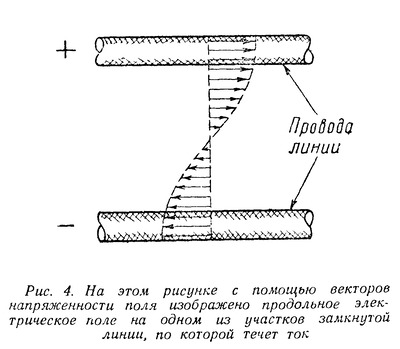 Направленное вдоль проводников электрическое поле изображено с помощью векторов на рис. 4. Для краткости мы дальше будем называть его продольным полем. Помимо продольного поля, связанного с падением потенциала вдоль проводников, существует также электрическое поле, связанное с наличием разности потенциалов между проводниками. Это поле, уже рассмотренное нами ранее в сечении, перпендикулярном проводам линии, изображено на рис. 2. Силовые линии здесь лежат в плоскостях, перпендикулярных к проводам. Поэтому для краткости дальше мы будем называть его поперечным полем. Полное электрическое поле между проводниками представляет собой результат наложения двух рассмотренных полей — продольного и поперечного. Продольное поле очевидно не изменит картины результирующего поля в сечениях, перпендикулярных к линии, и последнее в каждом таком сечении будет иметь такой же вид, как и на рис. 2. Лишь напряженность результирующего поля будет убывать по мере удаления от начала линии. В продольном же сечении результирующее поле примет иной вид. Наличие продольного поля приведет к тому, что силовые линии результирующего поля изогнутся (рис. 5). 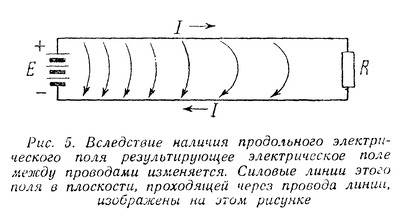 Влияние продольного поля будет сильнее там, где поперечное поле слабее, так как первое везде имеет одинаковую напряженность (мы считаем, что сопротивление проводов вдоль всей линии одинаково), а второе постепенно ослабевает к концу линии. Поэтому по мере приближения к концу линии силовые линии результирующего поля будут искривляться все сильнее и сильнее. Кроме того, результирующее поле будет ослабляться по мере ослабления поперечного поля, а значит и силовые линии его будут расположены к концу линии менее густо. Итак, в случае, когда в двухпроводной линии течет постоянный ток, картина электрического поля в продольном сечении линии (рис. 5) существенно отлична от той, которую мы получили для линии, разомкнутой на конце (рис. 3). Различие будет тем более заметно, чем больше падение напряжения в линии. Эти различия, как мы увидим в дальнейшем, весьма существенны для выяснения картины распространения энергии. Рассмотрим теперь магнитное поле вокруг двухпроводной линии, по которой течет постоянный ток. Силовые линии магнитного поля вокруг провода, по которому течет ток. имеют вид концентрических окружностей (рис. 6), причем направление этих линий определяется правилом буравчика (если вращать буравчик так, чтобы он ввинчивался в сторону движения тока, то направление вращения буравчика совпадает с направлением силовых линий). 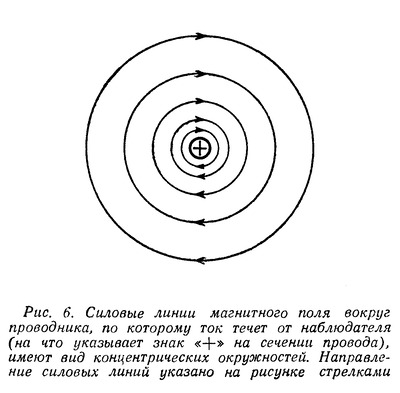 Напряженность магнитного поля убывает по мере удаления его от провода, в соответствии с чем уменьшается и густота силовых линий. От случая магнитного поля вокруг одного провода легко перейти к случаю двухпроводной линии. Магнитное поле такой линии представляет собой результат наложения магнитных полей, создаваемых токами, текущими в каждом из проводов. Так как эти токи текут в противоположные стороны, то и их магнитные силовые линии имеют противоположные направления. Легко установить, что между проводами направления силовых линий обоих полей оказываются одинаковыми, а по обе стороны от проводов они направлены навстречу друг другу. Поэтому между проводами оба магнитных поля будут усиливать друг друга, а во всем остальном пространстве — ослаблять друг друга. Следовательно, магнитное поле двухпроводной линии сосредоточено главным образом между проводами линии и быстро убывает по мере удаления от них (рис. 7). 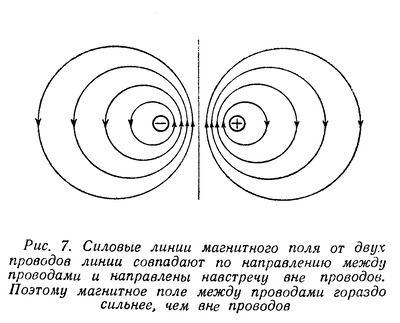 Распространение энергии вдоль двухпроводной линии Сопоставим теперь характер электрического и магнитного полей вокруг двухпроводной линии постоянного тока с картиной распространения энергии в такой линии. Сначала, для упрощения, положим, что сама линия не обладает сопротивлением. Если в линии нет потерь, то значит вся энергия, отдаваемая источником ЭДС, передается нагрузке. Присмотримся внимательнее, как происходит эта передача энергии. Поскольку вся энергия связана с электрическим и магнитным полями и эти поля в рассматриваемом случае сосредоточены преимущественно между проводами, то и энергия заключена главным образом в том же пространстве. Это значит, что энергия, отдаваемая источником, сразу в начале линии попадает в пространство между проводами и течет в нем от источника ЭДС к нагрузке. Энергия как бы «скользит» вдоль проводов, «опираясь» на них. Только на другом конце линии она снова «втекает» в нагрузку и рассеивается в ней (Вопрос о том, почему из источника ЭДС энергия вытекает в пространство между проводами, а на другом конце снова втекает в нагрузку, будет рассмотрен во второй части статьи). Значит сама передача энергии происходит не по проводам, а вдоль проводов линии. Таким образом, уже в этом простейшем воображаемом случае линии, не обладающей сопротивлением, видно, какую роль играют провода в процессе распространения электромагнитной энергии. Они отнюдь не передают энергию, а являются лишь «направляющими», вдоль которых течет энергия. Роль проводов выступает еще более отчетливо, если вместо воображаемой линии без сопротивления рассматривать линию реальную, обладающую сопротивлением. В этом случае внутри проводов линии существует продольное электрическое поле, тем более сильное, чем больше сопротивление проводов. Это электрическое поле, как и всякое другое, обладает энергией, часть которой сосредоточена в самих проводах, притом тем большая часть, чем больше их сопротивление. Внутри проводов существует и магнитное поле, и, следовательно, заключена часть магнитной энергии. Но характер этого магнитного поля не зависит от сопротивления проводов. Оно всегда мало по сравнению с полем между проводами и поэтому плотность энергии в нем гораздо меньше, чем в поле между проводами. Так как объем проводов мал, то и магнитная энергия внутри проводов всегда составляет очень малую долю всей магнитной энергии тока. Электрическое поле внутри проводника совершает работу по преодолению его сопротивления, и эта работа превращается в тепло. Следовательно, та энергия, которой обладает электрическое поле, сосредоточенное внутри проводника, не распространяется в нем, а расходуется на месте на нагревание проводника. Провода могут служить для передачи электромагнитной энергии лишь постольку, поскольку она сосредоточена вне проводников. Энергия же, попавшая внутрь проводника, на месте превратится в тепло, т. е. с точки зрения передачи энергии будет потеряна. Как видим, наличие сопротивления в линии изменяет картину распространения энергии по сравнению с линией без сопротивления в двух отношениях. Во-первых, изменяется характер электрического поля: появляется продольное поле, изменяющее конфигурацию результирующего поля вокруг линии. Во-вторых, изменяется картина течения энергии: по мере распространения последней вдоль линии часть энергии должна ответвляться и втекать в провода, где она превращается в тепло. Оба эти изменения в конфигурации электрического поля и в направлении течения энергии тесно связаны между собой. Здесь мы вплотную подошли к исходной идее Н. А. Умова, которая состоит в том, что должна существовать связь между конфигурацией электрического и магнитного полей и течением электромагнитной энергии. Исходя из этого, Н. А. Умов открыл те законы, которые связывают напряженность электрического и магнитного полей в данном месте с направлением и величиной потока электромагнитной энергии. Вектор Умова Чтобы установить связь между напряженностью электрического и магнитного полей, прежде всего необходимо пользоваться определенными характеристиками этих полей, с одной стороны, и потока электромагнитной энергии, с другой. Электрическое и магнитное поля, как указывалось, определяются векторами напряженности этих полей (векторами Е и Н, как мы будем их дальше называть для краткости). Поток электромагнитной энергии может быть охарактеризован с помощью векторной величины следующим образом. Направление вектора совпадает с направлением потока энергии, длина же его определяет величину потока, т. е. количество энергии, протекающей за единицу времени через ту или иную площадку. Однако при данном потоке количество протекающей энергии зависит от величины площадки и от ориентировки ее по отношению к потоку. Очевидно, чем больше площадка, тем больше протекает через нее энергии. С другой стороны, из двух одинаковых, но по разному ориентированных площадок, больше энергии протекает через площадку, расположенную перпендикулярно к потоку, чем через площадку, расположенную наклонно к нему. Чтобы дать вполне определенную количественную характеристику величины потока, принято указывать количество энергии, протекающей за единицу времени через расположенную перпендикулярно к потоку энергии площадку, поверхность которой равна единице. Эта величина называется плотностью потока энергии. Вектор, направление которого совпадает с направлением потока энергии, а длина соответствует плотности потока, впервые был введен в науку Н. А. Умовым и носит его имя. Наша задача заключается в том, чтобы установить связи между векторами напряженности электрического, магнитного полей и вектором Умова. Эту связь мы установим на конкретном примере двухпроводной линии, питаемой постоянным током, для которого мы уже выяснили, с одной стороны, картину электрического и магнитного полей, а с другой,— картину течения энергии. Прежде всего обратим внимание на следующее обстоятельство. Когда линия присоединена к источнику ЭДС, а второй ее конец разомкнут, между проводами линии существует электрическое поле, и значит распределена электрическая энергия. Однако энергия эта никуда не течет. Если же замкнуть второй конец линии на нагрузку, то энергия начнет течь от источника к нагрузке. Чем же различаются эти два случая с точки зрения характера электрического и магнитного полей вокруг линии? Почему в первом случае энергия не течет и вектор Умова везде равен нулю, а во втором случае энергия течет и значит вектор Умова в пространстве между проводами линии отличен от нуля? То, что при включении нагрузки несколько изменяется характер электрического поля (появляется продольное поле) не может играть существенной роли. В самом деле, если бы провода линии не обладали сопротивлением, то при включении нагрузки характер электрического поля оставался бы таким же, как и в случае линии, разомкнутой на конце. Между тем энергия не течет, когда линия разомкнута, и течет, когда линия замкнута на нагрузку, независимо от того, обладают провода сопротивлением или нет. Если провода не обладают сопротивлением, то единственное изменение, которое происходит при включения нагрузки, состоит в том, что помимо электрического появляется и магнитное поле (так как в линии возникает ток). Отсюда мы должны сделать первый важный вывод: энергия может течь в пространстве только в том случае, когда в этом пространстве существует как электрическое, так и магнитное поля. Иначе говоря, вектор Умова может быть отличен от нуля только в тех точках пространства, где отличны от нуля оба вектора Е и Н. Посмотрим теперь, как связаны между собой направления векторов Е и Н и вектора Умова. 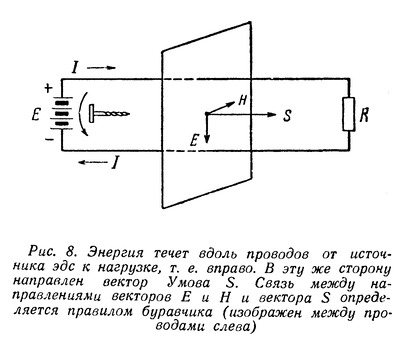 Для этого возвратимся к случаю, когда провода не обладают сопротивлением. Здесь (продольное поле отсутствует) векторы Е и Н лежат в плоскостях, перпендикулярных к проводам линии (рис. 8). Энергия же течет вдоль линии и так как потерь в ней нет, то одинаковое количество энергии протекает через любое сечение, перпендикулярное проводам линии. Это значит, что весь поток энергии направлен вдоль линии, т. е. вектор Умова (S) во всех точках, где присутствуют электрическое и магнитное поля, параллелен проводам линии. Следовательно, вектор Умова перпендикулярен плоскостям, в которых лежат векторы Е и Н, т. е. перпендикулярен к обоим этим векторам. Однако существуют два направления, перпендикулярные к данной площадке,— это направления в обе стороны от площадки. Поэтому нужно определить, в какую сторону от площадки направлен вектор Умова, при данном расположении на ней векторов Е и Н. Для нашего случая связь между расположением векторов Е и Н и направлением вектора Умова видна из рис. 8. Легко видеть, что при изменении направления одного из векторов Е или Н на обратное вектор Умова также меняет направление на обратное. Если же изменяется направление обоих векторов Е и Н на обратное, то направление вектора Умова остается неизменным. В этом последнем можно убедиться, изменив полярность источника ЭДС. Тогда изменится направление и электрического и магнитного полей между проводами (так как изменится и полярность проводов и направление тока). 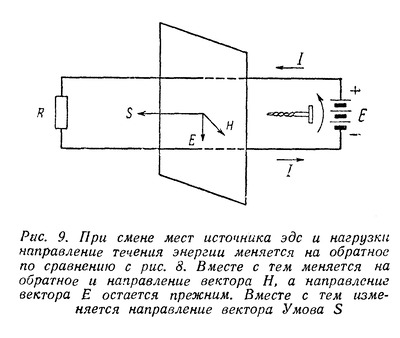 Если же поменять местами источник и нагрузку (рис. 9), то изменится Н, но не изменится направление Е. Вместе с тем изменится направление течения энергии на обратное по сравнению с тем, какое было в случае, изображенном на рис. 8, а значит и вектор Умова изменит направление на обратное. Связь между направлениями векторов Е и Н и вектора Умова во всех различных возможных случаях может быть охвачена одним общим правилом, именно — правилом буравчика. Если мы расположим буравчик так, чтобы его ручка лежала в плоскости векторов Е и Н и станем поворачивать ее от вектора Е к вектору Н, то направление, в котором начнет двигаться (ввинчиваться или вывинчиваться) буравчик, и будет направлением вектора Умова. Итак, вектор Умова перпендикулярен к векторам Е и Н и направлен по отношению к ним в сторону движения буравчика, поворачиваемого (кратчайшим путем) от Е к Н. Чтобы подкрепить и проиллюстрировать этот вывод, перейдем теперь от воображаемого случая проводов без сопротивления к реальным проводам, обладающим сопротивлением. В этом случае, как мы знаем, появляется продольное электрическое поле, и результирующее электрическое поле изменяет свой характер — его силовые линии искривляются, выгибаются в направлении от источника к нагрузке. Вектор Е этого поля вблизи проводов наклоняется у каждого из проводов в ту сторону, в которую течет ток (в направлении продольного поля — рис. 10). 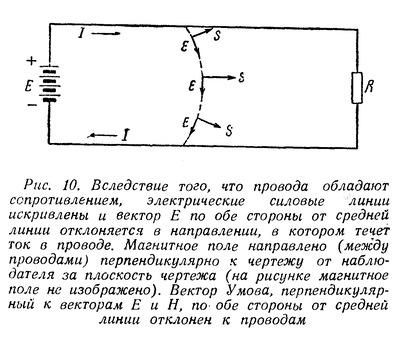 Магнитное же поле остается таким же, как и в случае проводов без сопротивления. Вместе с тем изменяется и направление течения энергии. Часть энергии, которая течет от начала линии, ответвляется по пути и втекает в провода, где превращается в тепло. Это значит, что вектор Умова в пространстве между проводами направлен вдоль проводов только на средней линии между проводами, а по обе стороны от средней линии он немного наклонен к проводам. Сопоставляя направление вектора Умова с расположением векторов Е и Н, легко видеть, что и в этом случае вектор Умова перпендикулярен к Е и Н и направлен по правилу буравчика. Именно потому, что вектор Е наклонен вперед у положительного провода и назад у отрицательного, вектор Умова у обоих проводов оказывается уже не параллельным проводам, а наклоненным к ним. Проследим теперь, как зависит величина вектора Умова от величины векторов Е и Н. Так как часть энергии теряется в проводах, то по мере удаления от источника ЭДС все меньше и меньше энергии протекает дальше, в сторону нагрузки. Значит поток энергии вдоль линии, а вместе с тем и величина вектора Умова вдоль линии должны уменьшаться. Отсюда видно, что величина вектора Умова убывает по мере уменьшения вектора Е (который зависит от падения напряжения вдоль линии). С другой стороны, если бы мы имели линию с теми же напряжениями, но иной силой тока, то поток энергии, а значит и величина вектора Умова были бы тем больше, чем больше сила тока, т. е. чем больше величина вектора Н между проводами линии. Более точное количественное рассмотрение подтверждает эти наши качественные выводы. Оказывается, что абсолютная величина вектора Умова пропорциональна произведению абсолютных величин векторов Е и Н. Кроме того, она зависит от угла между векторами Е и Н. Но мы ограничимся только простейшими случаями, когда векторы Е и Н приблизительно перпендикулярны друг другу (что имеет место между проводами двухпроводной линии и в других случаях, которые мы будем рассматривать). Итак, вектор Умова перпендикулярен векторам Е и Н, направлен по буравчику, поворачиваемому от Е к Н, и по абсолютной величине пропорционален произведению абсолютных величин Е и Н. Пользуясь вектором Умова, мы в дальнейшем рассмотрим другие случаи распространения энергии, помимо двухпроводной линии с постоянным током. А сейчас, несколько забегая вперед, укажем, что во всех случаях энергия распространяется не по проводам, а вдоль проводов. Образно выражаясь, провода линии это не трубы, по которым энергия течет, а рельсы, вдоль которых она скользит. Так обстоит дело не только в случае двухпроводной линии и постоянного тока, но и во всех других случаях. Электромагнитная энергия не может распространяться по проводникам, а лишь только вдоль них. В самих проводниках энергия неизбежно рассеивается, превращаясь в тепло. Проводники электричества не являются «проводниками энергии», а лишь «направляющими», вдоль которых энергия может течь. Правда, в случае постоянного и низкочастотных токов, без этих «направляющих» энергия вообще не может распространяться на большие расстояния. В случае же высокочастотных токов энергия может распространяться и без направляющих. Но все же, несмотря на это существенное различие, роль «направляющих», т. е. проводников, во всех случаях одна и та же, а именно: они обеспечивают такую конфигурацию электрических и магнитных полей, при которых становится возможным распространение электромагнитной энергии в определенном направлении. Именно с этой единой точки зрения целесообразно рассматривать различные случаи распространения электромагнитной энергии. (Окончание см. здесь) Автор: С. Хайкин Источник публикации: ж. Радио, 1951, № 7, с. 43 - 48 | |
| Просмотров: 4136 | |